

Selecting and defining a tiny strip of mass with differential width. M.O.I relative to the origin, Jo = Ix + Iy = ⅛ πr 4 + ⅛ πr 4 = ¼ πr 4 Now to find the moment of inertia of the semicircle we will take the sum of both the x and y-axis.
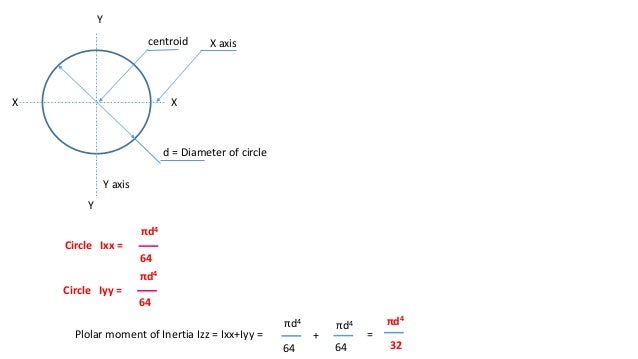
Moment of inertia of a circle about its centroid full#
Thus, M.O.I will be half the moment of inertia of that of a full circle. Here, the semi-circle rotating about an axis is symmetric, and therefore, we consider these values equal.
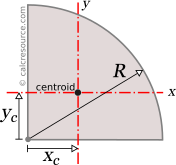
Thus similarly for the semicircle, the moment of inertia of the x-axis is equal to that of the y-axis. Now we need to pull out the area of a circle which gives us: M.O.I relative to the origin, Jo = Ix + Iy = ¼ πr 4 + ¼ πr 4 = ½ πr 4 We know that for a full circle because of complete symmetry and uniform area distribution, the moment of inertia relative to the x-axis is equal to that of the y-axis. Further to determine the moment of inertia of the semi-circle, we will take the sum of both the x and y-axis.
The moment of inertia of the semicircle is generally expressed as I = πr 4 / 4.Here in order to find the value of the moment of inertia of a semicircle, we have to first derive the results of the moment of inertia full circle and basically divide it by two to get the required result of that moment of inertia for a semicircle. The moment of inertia of the semicircle is generally expressed as I = πr 4 / 4 Similarly larger the moment of inertia of the body more difficult is to stop its rotational motion. For example, if the body is at rest the larger the moment of inertia of the body the more difficult it is to put the body into the rotational motion. In other words, the moment of inertia is the measurement of resistance of the body to a change in its rotational motion. The most straightforward approach is to use the definitions of the moment of inertia (10.1.3) along with strips parallel to the designated axis, i.e.The moment of inertia plays the same role in rotational motion as the mass does in the translational motion. We will use these observations to optimize the process of finding moments of inertia for other shapes by avoiding double integration. We saw in the last section that when solving (10.1.3) the double integration could be conducted in either order, and that the result of completing the inside integral was a single integral. Of course, the material of which the beam is made is also a factor, but it is independent of this geometrical factor. A beam with more material farther from the neutral axis will have a larger moment of inertia and be stiffer. The shape of the beam’s cross-section determines how easily the beam bends. The appearance of \(y^2\) in this relationship is what connects a bending beam to the area moment of inertia. This moment at a point on the face increases with with the square of the distance \(y\) of the point from the neutral axis because both the internal force and the moment arm are proportional to this distance. Think about summing the internal moments about the neutral axis on the beam cut face. The internal forces sum to zero in the horizontal direction, but they produce a net couple-moment which resists the external bending moment.įigure 10.2.5.Internal forces in a beam caused by an external load. The change in length of the fibers are caused by internal compression and tension forces which increase linearly with distance from the neutral axis. The neutral axis passes through the centroid of the beam’s cross section. The points where the fibers are not deformed defines a transverse axis, called the neutral axis. Fibers on the top surface will compress and fibers on the bottom surface will stretch, while somewhere in between the fibers will neither stretch or compress. When an elastic beam is loaded from above, it will sag. Assume that some external load is causing an external bending moment which is opposed by the internal forces exposed at a cut. To provide some context for area moments of inertia, let’s examine the internal forces in a elastic beam.


 0 kommentar(er)
0 kommentar(er)
